Hintergrundwissen: Energy Time Curve (ETC)
Zielgruppe
Alle, die ein gewisses technisch naturwissenschaftliches Interesse haben und das Kapitel Hintergrundwissen bereits gelesen haben. Alle, die den Zusammenhang von Reflexionen und Impulsantwort genauer verstehen möchten.
Reflexionen finden
Die ETC (Energy Time Curve, auch Impulse Response Envelope) wird aus der Impulsantwort berechnet. Genauer gesagt ist hier die Hilbert Transformierte gemeint. Andere Anbieter benutzen die Bezeichnung für den Logarithmus der quadrierten Impulsantwort (Log-Squared-ETC). Letztere hat bei Hifi-Apps keinen eigenen Namen, sie wird bei der Ansicht "Logarithmisch" / [RAW] ausgegeben.
Die ETC soll die Maxima durch Reflexionen deutlicher hervorheben als die Rohdaten, indem sie andere Maxima unterdrückt. Aus dem Abstand zwischen den Peaks von Direktschall und Reflexion kann der Umweg der Reflexion in Metern abgelesen werden - wie bei der Bodenreflexion in geometrischen Akustik. Danach kann man die "Schnur-Methode" verwenden, um die reflektierende Fläche zu finden. Man spannt dazu eine Schnur zwischen Mikrofon und Lautsprecher (im Zweifel dem Mittel- oder Hochtöner) und verlängert sie danach um diesen Umweg. Findet sich jetzt eine Fläche, in der sich a) der Lautsprecher am Messplatz spiegeln würde, wenn sie aus Glas wäre und die b) mit der gespannten Schnur am Reflexionspunkt (mit 10 oder 20 cm Toleranz) berührt werden kann, dann verursacht diese höchstwahrscheinlich die Reflexion.
Im nächsten Schritt kann dort versuchsweise Dämmmaterial angebracht und geprüft werden, ob sich Klang und Messwerte verbessern. Dabei sollte im Zweifel nicht mit der Dicke des Dämmmaterials gespart werden: Schmale angezeigte Peaks sind besonders auffällig in den Messdaten, sie entstehen aber technisch gesehen nur durch die Spiegelung der höchsten Frequenzen. Dünnes Dämmmaterial lässt sie im Output verschwinden, mit den oberflächlich freundlicheren Messwerten wird sich der Klang vielleicht sogar verschlechtern [Zehner]. Die Anbieter von Dämmmaterial geben den jeweiligen Frequenzbereich für ihre Produkte an. Wer mit der Materie nicht vertraut ist, sollte mindestens bis 1 kHz hinunter, besser noch deutlich tiefer, dämmen. Vor der Bestellung kann die Fläche probeweise mit Kleidung oder Bettzeug gedämmt werden. Daumenregel: Für eine gewisse Wirkung bis 1 kHz sollte letzteres eine Dicke von $\lambda/4\simeq 10 $cm haben, dicker wäre sicher besser.
Die ETC alleine ist kein Patentrezept zur Darstellung von Reflexionen, die folgenden Abschnitte sollen deshalb einen Überblick über den technischen Hintergrund und das optimale Zusammenspiel mit Glättung und anderen Darstellungen geben.
Druck und Schnelle
Eine Resonanz kann man sich als Zusammenspiel zwischen Hin-und-Her-Bewegung (Schnelle) und Druck der
Luft vorstellen. Sehr einfach ist das bei Wellen, die sich nicht ausbreiten, z.B. bei dieser
Raummode:

In der Bildmitte herrscht maximale Schnelle während der Druck sich kaum ändert. Am Bildrand ist das Gegenteil
der Fall. Die Energie steckt abwechselnd in der Bewegungsenergie der Luft in der Raummitte und im Druckunterschied
zwischen den Bereichen nahe der Wände.
Bei einer propagierenden Welle die, die sich von der Schallquelle aus ausbreitet, ist dieses Zusammenspiel
zwar etwas komplizierter, dadurch ändert sich die grundlegende Idee aber nicht.
Nun könnte man davon ausgehen, dass bei einer Reflexion der Schall von der Quelle zeitversetzt ein weiters mal ankommt und dass deshalb jeder Peak oder größere Ausschlag in der Impulsantwort einer Reflexion entspricht. Hätten zufällig mehrere Reflexionen den gleichen Umweg und damit die gleiche Laufzeitverzögerung (z.B. an Wand und Boden), wäre das mit verschiedenen Mikrofonpositionen leicht zu beherrschen. Tatsächlich funktioniert diese Methode auch manchmal ganz gut, es gibt nur ein grundlegendes Problem: Sowie der Schall eine Resonanz im Raum anregt (also eigentlich immer), entsteht eine Schwingung die man in der Impulsantwort auch als solche sehen kann (siehe zahlreiche Bilder bei Messungen).
Die Impulsantwort ist auch Null, wo diese Schwingung Nulldurchgänge hat. Und durch den Wellencharakter entstehen drumherum Maxima und ein Minima. Üblicherweise arbeitet man mit dem logarithmierten Betrag - dort würden sich mehrere Maxima zeigen, die sich kaum von dicht beieinanderliegenden echten Reflexionen unterscheiden. In der Praxis ist es dadurch beispielsweise problematisch zu unterscheiden, ob mehrere getrennte Peaks eine einzelne Reflexion oder mehrere unabhängige Reflexionen anzeigen [Zehner].
Ein Lösungsvorschlag wurde in [Heyser 1971] veröffentlicht. Sowohl unser Ohr als auch gängige Mikrofone reagieren nur auf den Druck-Anteil der Welle, Schnelleempfänger werden kaum verwendet. Dadurch kann es letztlich zu den irreführenden Ergebnissen kommen: Herrscht an einem bestimmten Messplatz für eine bestimmte Frequenz Stille kann es bedeuten, dass dort a) wirklich keine Schallenergie ist oder b) der Großteil der Energie in der Schnelle steckt, wie etwa in der Mitte der Animation oben. Der gemessene und hörbare Schalldruck ist dort am rechten und linken Rand am höchsten.
Die gemessene und angezeigte Impulsantwort enthält also "nur die direkt relevante, hörbare Hälfte" der physikalischen Energie. Intuitiv ist klar, dass die "andere Hälfte", d.h. die Schnelle genauso wichtig ist: Wäre sie in der Mitte der Animation Null, gäbe es keinen Schalldruck am Rand. Heyser setzt mit Energierehaltung für alle Fourier-Komponenten der Welle an und ergänzt den fehlenden Teil mit einem mathematischen Kunstgriff (s.u.). Als Ergebnis werden korrelierte Schallkomponenten geglättet, während singuläre ihre Form behalten. Die "Wellen" gehen verloren, die Reflexionen bleiben. Die physikalisch Schallenergie wird dadurch nicht widergespiegelt, sie ist in einer propagierenden Welle nicht gleichmäßig verteilt. Ziel der Methode ist vielmehr kohärente Welligkeiten durch Resonanzen zu glätten und dabei inkohärente Störungen durch Reflexionen unbeeinflusst zu lassen. Laut Heyser ist die ETC nicht als Einhüllende, sondern als das volle, komplexe analytische Signal zu sehen. Die folgenden Bilder zeigen einige Stärken und Schwächen dieser Vorgehensweise.
Grundlage sind 3 Logsweeps, die per Wave-Editor zeitversetzt addiert wurden. Diese wurden der App als Mikrofonsignal "vorgegaukelt". Damit soll der Direktschall eines Lautsprechers und zwei verzögert eintreffende Ereignisse simuliert werden. Die Reflexionen liegen jeweils 2 ms auseinander, das entspricht 0.68 und 1,37 m zusätzlichem Weg, also z.B. einer Reflexion an Wand und am Boden. Der erste Logsweep wurde unbearbeitet gelassen, die beiden reflektierten Logsweeps wurden bei 1 kHz mit 12 dB/Oktave abgeschnitten. In der Praxis könnte das durch einen Teppich oder Schaumstoff in einem Möbelstück verursacht werden. Ziel ist, die beiden Reflexionen trotzdem möglichst sicher zu erkennen.
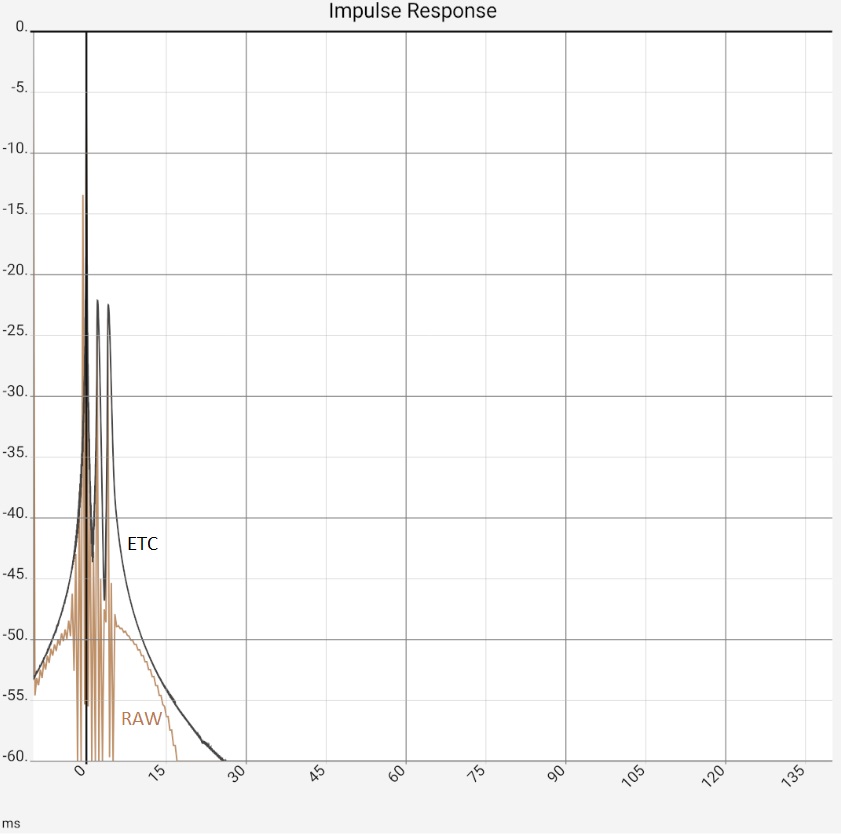
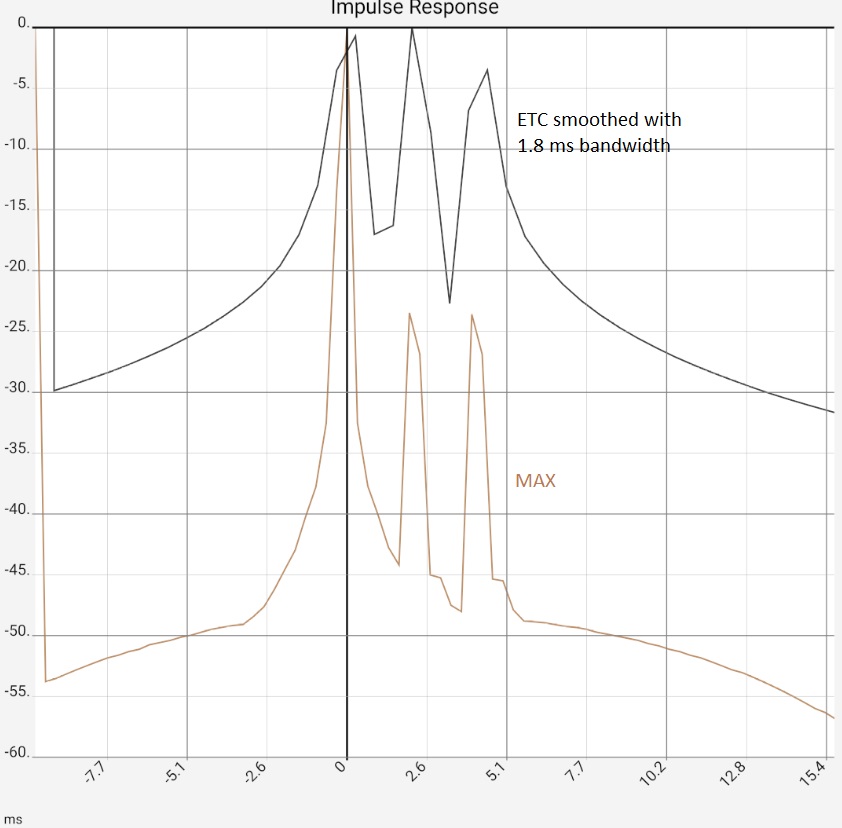
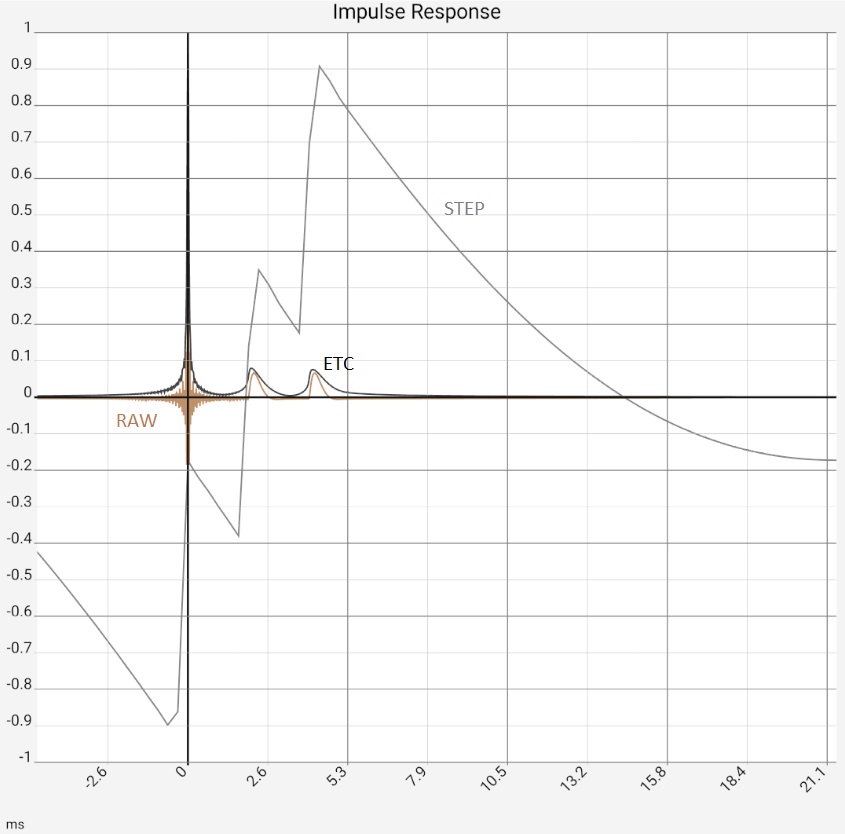
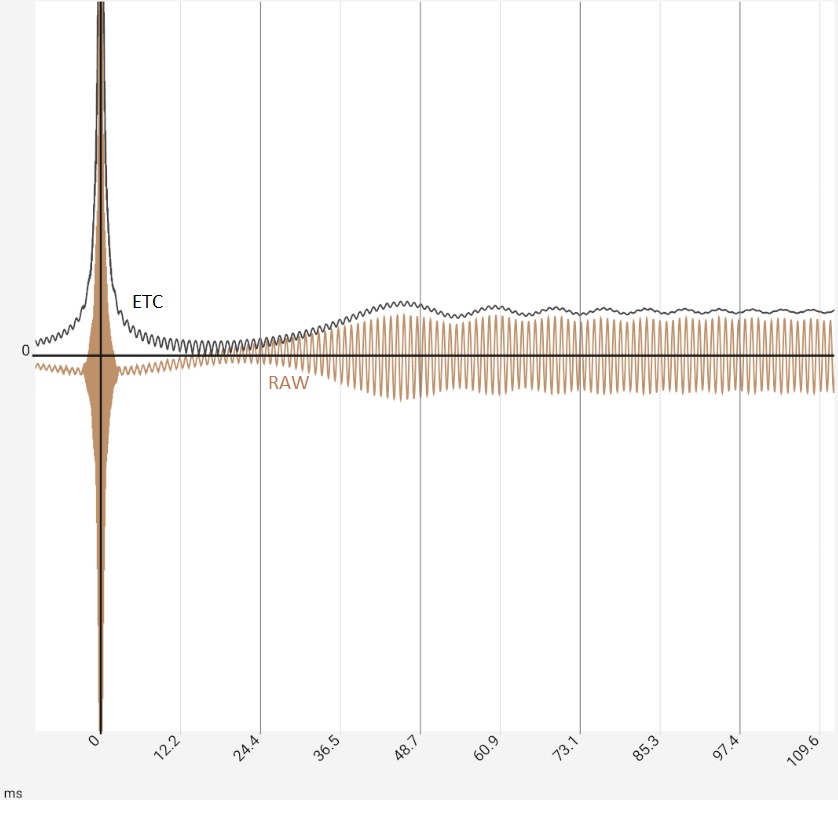
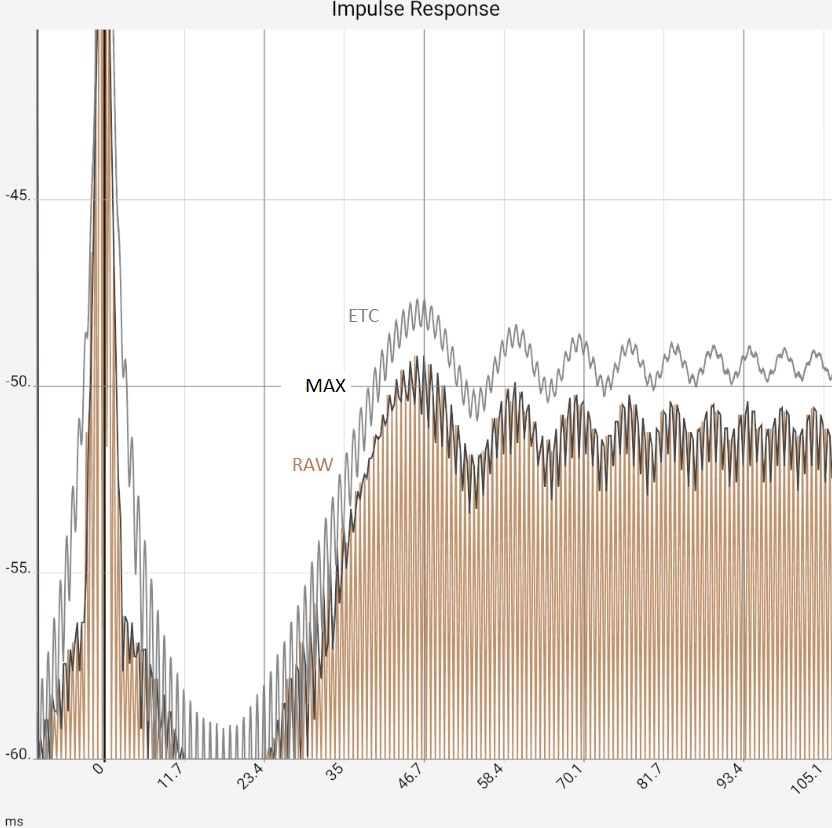
Das erste Bild stellt die Situation nach Programmstart dar, in der Praxis wären die beiden Peaks durch die Reflexionen typischerweise etwas höher bei -10...-20 dB, da sie mehr höhere Frequenzkomponenten enthielten und dadurch entsprechend "peakartiger" wären. Bild 2: Nach Zoom und Umschalten von Rohdaten [RAW] auf Maximalwerte [MAX] wäre klar, "dass da was ist". Die ETC arbeitet die Peaks das heraus, bringt aber keine neuen Erkenntnisse gegenüber einem Umschalten auf [MAX]: Die App zeigt dann nur die Maximalwerte (von 0.5 ms-Abschnitten) der Impulsantwort. Die Stufen in der braunen Kurve entstehen durch Zusammenspiel von Auflösung und Zoom, sind also ein technisches Artefact. Völlig geglättet ist dagegen die hochfrequente Schwingung um den ersten Peak herum. Diese entsteht durch die Begrenzung des Frequenzgangs (siehe weiter unten), aber auch das ist durch [MAX] genauso. Im dritten Bild wurde die ETC zusätzlich geglättet, wodurch der erste Peak bei 0 entsprechend abgeflacht wurde. Da das Maximum auf 0 dB festgelegt bleibt, treten die beiden Reflexionen jetzt deutlich hervor. Das letzte Bild zeigt die selben Daten in linearer Darstellung. Die beiden Reflexionen sind in den Rohdaten jetzt leicht zu übersehen, weil Ihnen durch die fehlenden hohen Frequenzkomponenten die "Peakigkeit" verloren gegangen ist. Die Reflexionen werden ab besten durch die STEP-Kurve herausgearbeitet, die sich aus dem Integral der Rohdaten berechnet. Die Fläche unter den kleinen Buckeln durch die Reflexionen ist vergleichbar mit der unter dem ersten Peak.
In diesem Fall bringt die ETC also praktisch keinerlei Erkenntnisse, Glättung oder [STEP] Funktion sind der bessere Weg. Das umgekehrte Bild zeigt sich, wenn das Mikrofon-Signal durch einen Logsweep (2 Sek, 20 Hz - 20 kHz) ersetzt wird, zu dem zusätzlich (ab ca. 1.1 sek) ein 1 kHz Signal mit gleichem Pegel addiert wurde. Letzteres soll den Extremfall einer Resonanz darstellen, vielleicht durch einen Lüftungskanal:
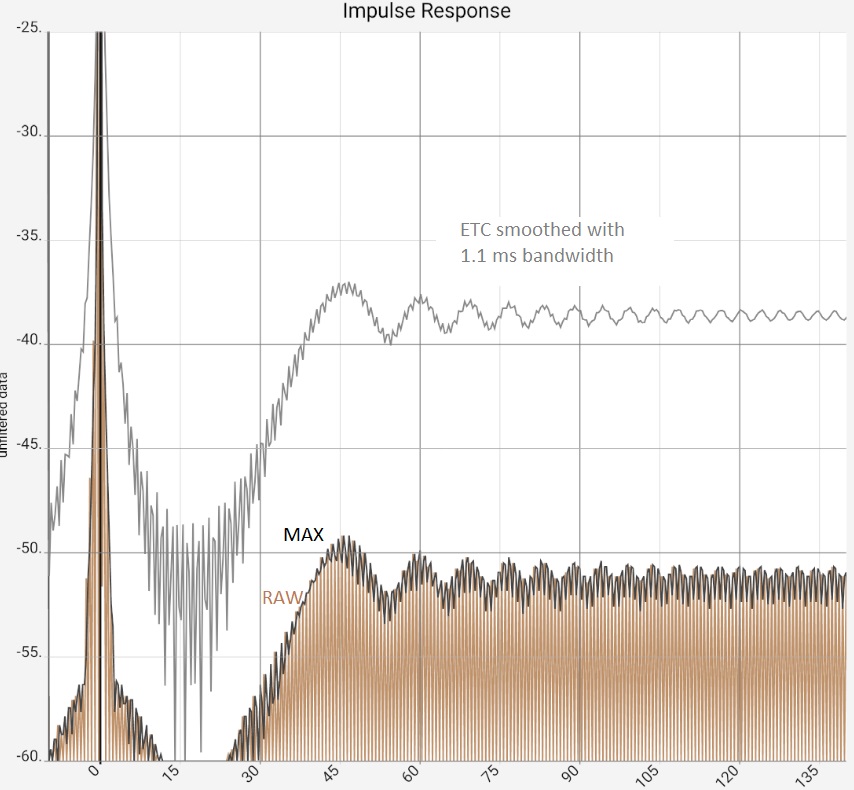
Bild 1 und 2: Hier kann die ETC ihre Fähigkeiten ausspielen: Das 1 kHz Signal (braun) ist durch die hohe Kohärenz optimal zu erfassen und wird nahezu vollständig geglättet (grau). Bild 3: Auch Logarithmierung und Maximalwertbildung liefern kein vergleichbares Ergebnis. Bild 4: Mit einer gewissen Vorahnung, welche Frequenzen reflektiert werden, kann zusätzlich eine angemessene Glättung für ETC ausgewählt werden. Damit wird die Qualität der ETC-Ausgabedaten nochmals verbessert. Die Filterung des Signals, z.B. mit einem Tiefpass bei 2 kHz liefert in diesem Beispiel ähnliche Ergebnisse, könnte in der Praxis aber weitere Verbesserungen ermöglichen.
In der Praxis wird die ETC von manchen Toningenieuren als wichtiger Teilaspekt herangezogen für mehr Sicherheit bei der Interpretation gemessener Reflexionen. Ein wirklicher Gewinn ist erst im Zusammenspiel mit Filterung, Glättung und anderen Darstellungen zu erwarten.
Technischer Background
Heyser setzt mit Energieerhaltung für alle Fourierkomponenten der Welle an, fügt also anschaulich gesprochen dem sinusförmigen Verlauf des Drucks einen cos-Term für die Schnelle hinzu, damit die Gesamtenergie wegen $\sin^2x + \cos^2x = 1$ konstant bleibt. Dadurch wird eine gleichmäßige Energiedichte über den Wellenzug jeder Fourierkomponente erreicht und störende Nulldurchgänge in der Impulsantwort fallen weg. In der Praxis erhält man solch einen Sachverhalt z.B. im Kundtschen Staubrohr, eine propagierende Welle hat keine gleichmäßige Energiedichte. Die ETC repräsentiert also nicht die wirkliche, messbare Energiedichte.
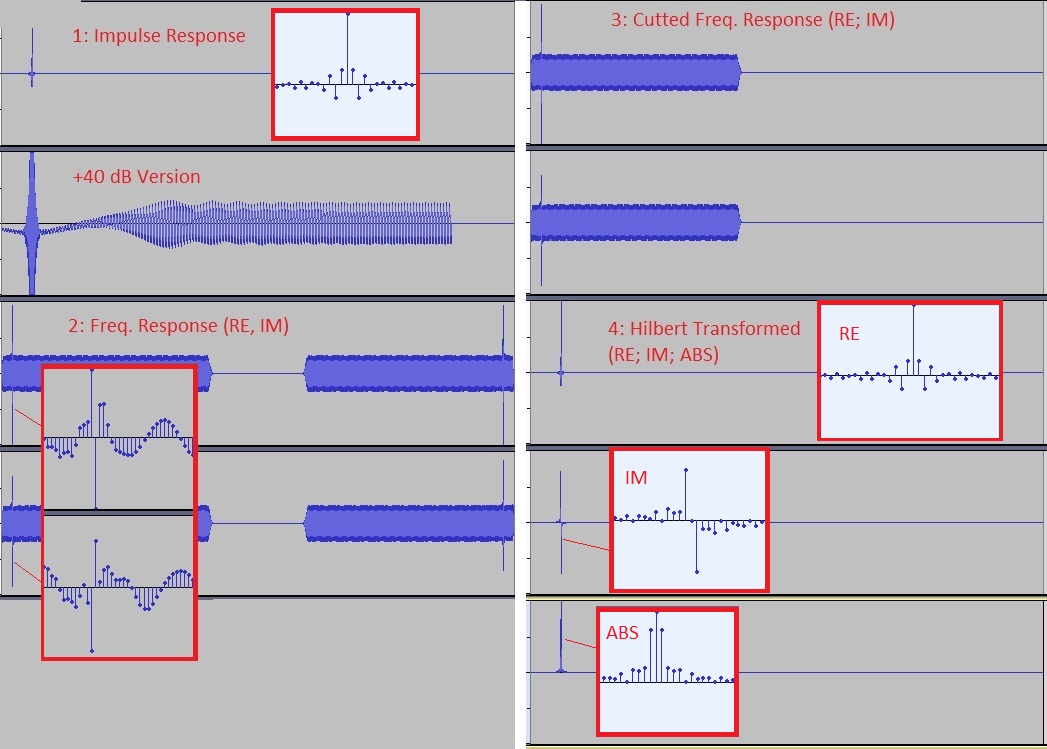
Die Berechnung soll hier an einer künstlich hergestellten Impulsantwort veranschaulicht werden: Das Mikrofon-Signal wurde durch einen Logsweep (2 Sek, 20 Hz - 20 kHz) ersetzt, zu dem zusätzlich (ab ca. 1.1 sek) ein 1 kHz Signal mit gleichem Pegel addiert wurde.
1: Das 1 kHz Signal ist in der Impulsantwort (nach 40 dB Verstärkung) zu sehen und stellt die missverstandene Reflexion dar: Jedes Maximum hat Ähnlichkeit mir einer Reflexion und erschwert damit die Interpretation.
2: Per Fouriertransformation wird der Frequenzgang berechnet, die Peaks bei 1 kHz sind im Realteil und Imaginärteil deutlich erkennbar. Da die Impulsantwort reellwertig war, sind Realteil und Imaginärteil (gerade und ungerade) spiegelsymmetrisch.
3. Es geht also keine Information verloren, wenn der rechte Teil entfernt wird. Anschaulich gesehen geht dadurch aber im Fourierraum jedem $\exp(i\omega t)$ der jeweilige gespiegelte Term $\exp(-i\omega t)$ verloren, so dass bei der Rücktransformation statt $\sin$ bzw. $\cos$ Termen jetzt $\exp(i\phi)$-Terme auftreten, deren Betrag konstant ist. Vergrößert man das Ergebnis, ergibt sich ein entsprechendes Bild:
4. Im Letzten Schritt erfolgt die Rücktransformation. Durch die neuen Terme entsteht jetzt ein Imaginärteil, die App gibt das als Ergebnis den Absolutbetrag aus. In der Vergrößerung ist zu erkennen, dass sich die FWHM des Peaks durch den hinzukommenden Imaginärteil um 2 Samples verbreitert: In Schritt 1 ist der Peak 1 Sample breit, es folgt kurzes hochfrequentes Filterklirren weil der Sweep bei 20 kHz endet. Bei Schritt 4 beträgt die FWHM 3 Samples. Trotzdem kann gesagt werden, dass durch die Operation keine Auflösung verloren geht: Die Verbreiterung beträgt 2 Samples, d.h. ihr physikalischer Wert in ms beträgt bei 48000 Samples/s 0.042 ms bzw. bei 192k 0.01 ms, bzw. 3 mm Schalllaufzeit. Es handelt sich also um ein Artefact der begrenzten Auflösung und keine Problematik der Methode.
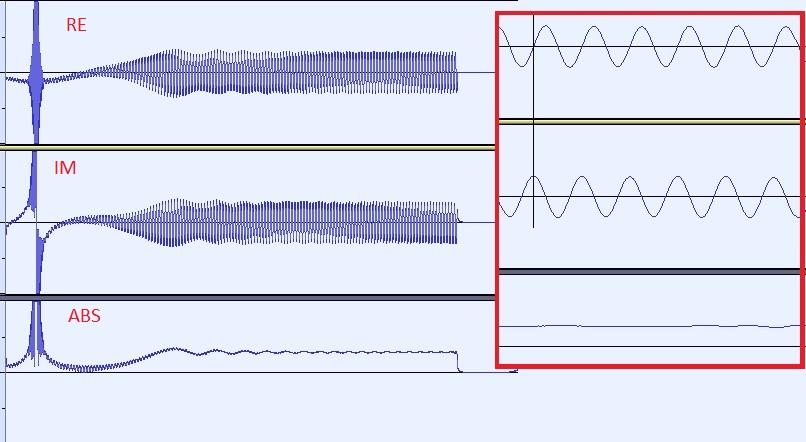
Ein Zoom auf das Ergebnis (Schritt 4) zeigt: Real- und Imaginärteil sind im $\pi/2$ phasenverschoben, der Betrag ist konstant genug, um nicht als Reflexion interpretiert zu werden.
Literatur
[Heyser 1971] Heyser, Richard: Determination of Loudspeaker Signal Arrival Times - Part III. J. Audio Eng. Soc. 19, 902 (1971). Abgedruckt in "An anthology of the works of Richard C. Heyser on measurement, analysis, and perception" AES - Time Delay Spectroscopy, Seite 44ff, 57ff
[Zehner] Markus Zehner: "Messungen und Interpretation von ETCs / Reflektierte Fehlschlüsse" www.zehner.ch/lab/etc.html, www.zehner.ch/lab.html